Función par
Una función par es cualquier función que satisface la relación f(x)=f(-x) y si x es del dominio
de f entonces -x también.
Desde un punto de vista geométrico, una función par es simétrica con respecto al eje y, lo que quiere decir que su gráfica no se altera luego de una reflexión sobre el eje y.
Ejemplo:
Función impar
Una función impar es cualquier función que satisface la relación:
Desde un punto de vista geométrico, una función impar posee una simetría rotacional con respecto al origen de coordenadas, lo que quiere decir que su gráfica no se altera luego de una rotación de 180 grados alrededor del origen.
Ejemplos de funciones impares son x, x3, seno(x), sinh(x), y la erf (x).
Ejemplo
La función: .
. Si vemos la función:
Si vemos la función:






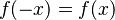










No hay comentarios:
Publicar un comentario